Problem Statement
Hearing loss is a problem that affects millions of people. In order to alleviate the problem, many patients wear hearing aids that contain audio processing algorithms with lots of tuning parameters. Since hearing loss profiles are unique for each individual, it is hard to find the best hearing aid settings for a given patient, especially when unforeseen hearing problems may arise in-the-field.
We aim to automate hearing aid algorithm design under in-situ conditions and argue that a proper hearing aid design agent (HADA) should be able to support the following tasks:
- describe in-situ hearing aid design as a personalized incremental tuning process;
- decide which signal processing circuit to use for hearing loss compensation;
- estimate the tuning parameters of a given signal processing algorithm;
- evaluate the performance of a given signal processing algorithm relative to an alternative algorithm.
Methods and Solution Proposal
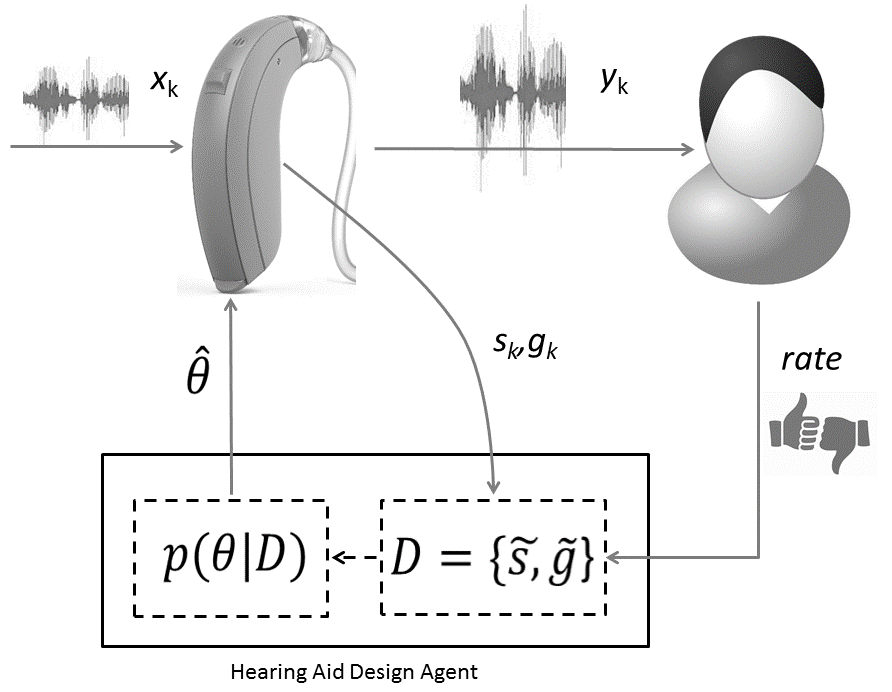
The architecture of our proposed solution method is sketched in Fig.1. Under in-situ conditions, HADA receives both a HA module’s input ($s_k$) and output signals (the gain $g_k$). Moreover, once in a while, HADA receives a thumbs-up or thumbs-down appraisal from the patient. A positive patient evaluation triggers HADA to execute an incremental update of the distribution over hearing aid parameters (i.e., it updates $p(\theta|D)$), while a negative evaluation prompts HADA to send alternative parameter settings ($\hat \theta$) to the hearing aid, thus starting a new listening trial. Note that in this way, hearing aid design becomes an always-on learning process of consecutive trials. The challenge for HADA is to learn to propose interesting alternative HA algorithms whenever the patient is unhappy about his current listening experience. We used a fully Bayesian approach to infer both the signal processing algorithm, the HA parameter settings, the performance evaluation task and for deciding the next best alternative algorithm.
Results
In order to illustrate the process of personalized in-situ hearing aid design, we simulated HADA’s execution of the signal processing, parameter estimation and model comparison tasks.
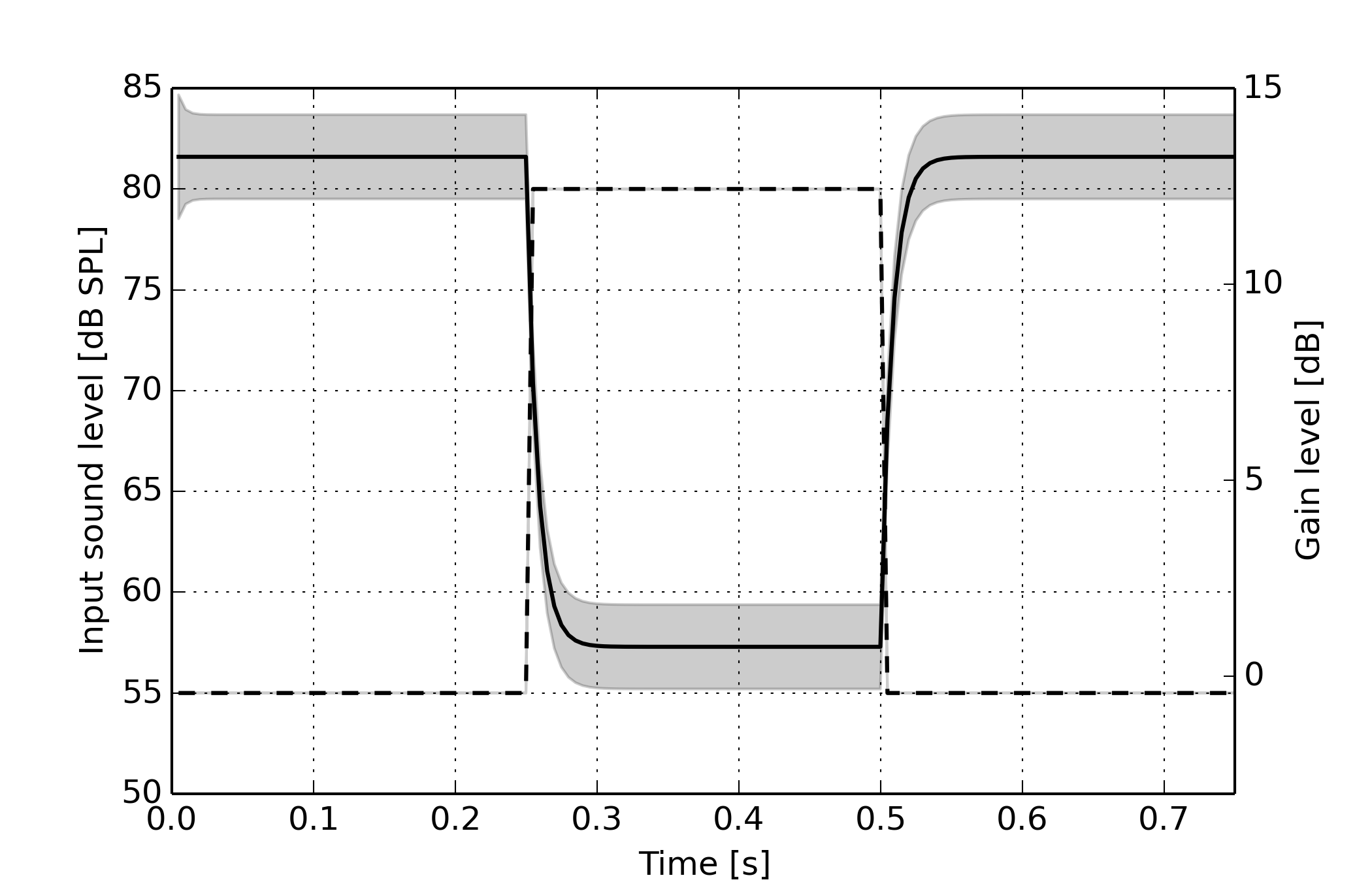
For the signal processing task, we challenged HADA to infer a personalized hearing loss compensation algorithm, based on a received audio signal (by the HA microphones) and a generative probabilistic hearing loss model. The results are plotted below for a piecewise linear hearing loss model (in the log-power domain) in a single (arbitrary) frequency band, with a hearing threshold at 45 [dB HL], and a recruitment threshold at 90 [dB HL]. Here, the dashed line represents the input sound level, and the solid line the inferred compensation gain. We notice that HADA is able to generate a signal processing algorithm that exhibits the behaviour of a dynamic range compressor.
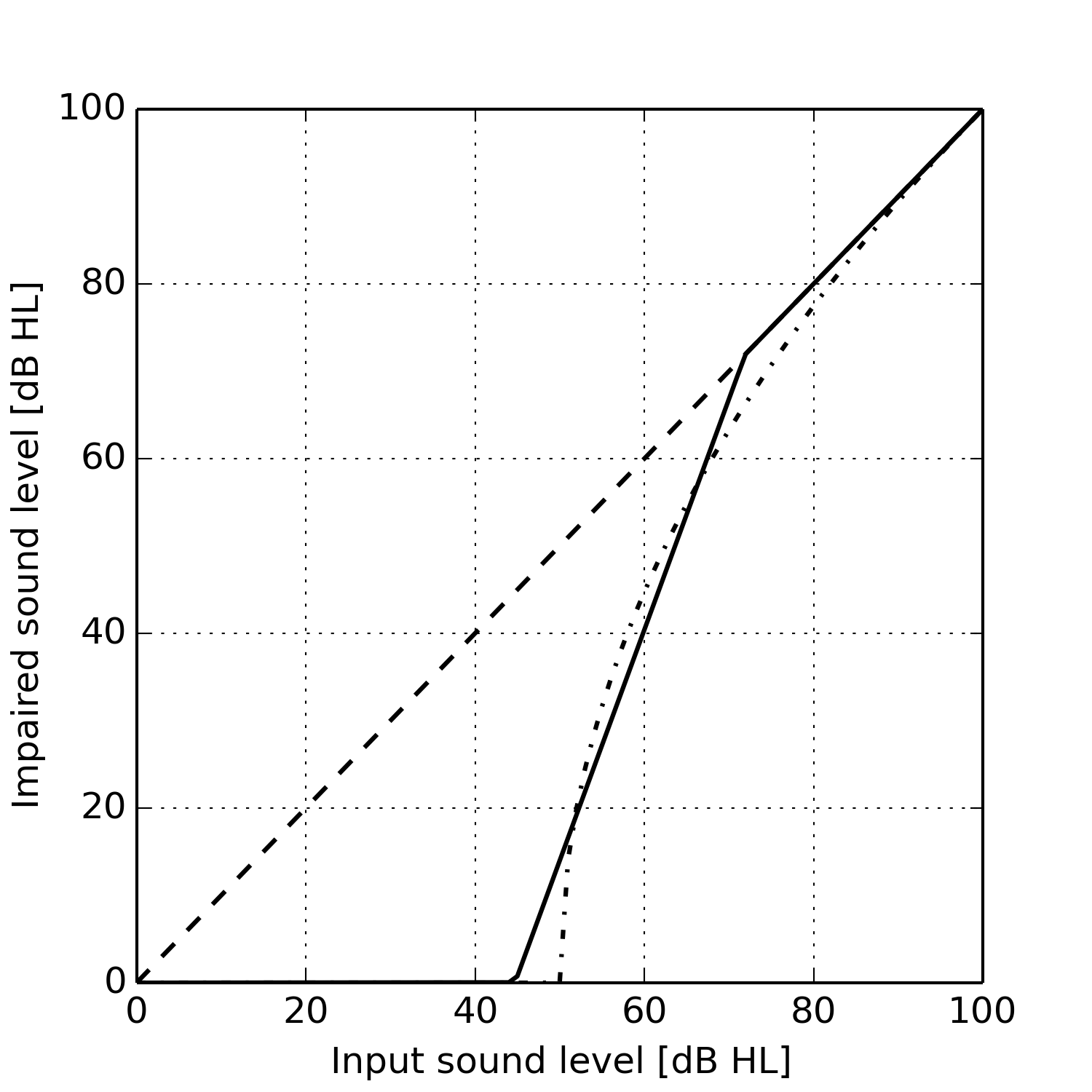
For the parameter estimation task, the challenge for HADA was to learn the parameters for a HA module with given piecewise-linear hearing loss model. We used a complex latent hearing loss model to generate a training data set for the HA module’s input and output signals. The figure below shows a close fit between the piecewise-linear model (solid curve) to the complex latent model (dash-dotted curve). Thus we found that an appropriate hearing loss model (and algorithm) can be learned straight from audio data.
For model comparison, HADA was tasked to evaluate the performance of an alternative hearing loss compensation algorithm relative to a reference algorithm. The alternative algorithm contained a mechanism that limits distortion on the inferred gains. The reference algorithm did not contain this mechanism. HADA estimated the Bayes Factor between both algorithms, based on a given training set of input-gain signal pairs. The alternative algorithm outperformed the reference algorithm by 16.7 [dB]. This example illustrates that the Bayes factor can be used as a performance metric for competing audio processing algorithms.
Reference
Thijs van de Laar and Bert de Vries (2016). A Probabilistic Modeling Approach to Hearing Loss Compensation. IEEE Tr. on Audio, Speech and Language Processing 24(11), 2200-2213.