Bayesian Pure-tone Audiometry

Problem Statement

The pure-tone hearing threshold - the lowest sound intensity that a person can perceive - is usually estimated from responses to stimuli at a set of standard frequencies. At each frequency, a staircase ‘up 5 dB - down 10 dB’ approach is used to incrementally estimate the threshold level. This simple approach however suffers from a number of drawbacks:

  • It does not provide an uncertainty measure for the estimated thresholds.
  • It is difficult to exploit potential prior knowledge about the threshold curve.
  • It is data-inefficient because it does not exploit the correlation between the thresholds at different frequencies.
  • Restricting the stimuli to a fixed set of standard frequencies requires additional assumptions (such as piecewise linearity) to obtain the complete hearing threshold curve (as a function of frequency).

This project aims to address these problems by taking a probabilistic approach to the pure-tone hearing threshold estimation problem.

Methods and Solution Proposal

One can view the threshold estimation problem as a probabilistic inference problem. To that end, we put a Gaussian process prior on the hearing threshold curve. Moreover, we model the user’s responses to stimuli by a probabilistic response model. This model describes how the user response depends on their hearing threshold and the presented test tone. Given the response model, approximate Bayesian inference techniques are applied to approximate the posterior distribution of the hearing threshold.

This results in a “Bayesian pure-tone audiometry” method illustrated by the figure below. 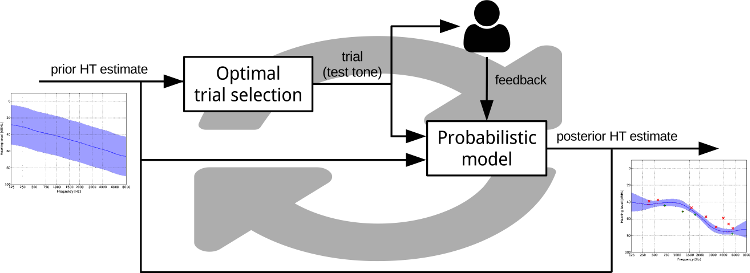png The Bayesian pure-tone audiometry method incrementally decreases the uncertainty about the users hearing threshold curve by repeating the following steps:

  1. Use the current (uncertain) estimate of the HT curve to determine the ‘optimal’ (most informative) next test tone. This tone is not restricted to a set of standard frequencies.
  2. Play the test tone and collect the user’s binary response: audible or non-audible.
  3. Update the probabilistic estimate of the HT curve (i.e. approximate the posterior GP) based on the data collected so far.

These steps are repeated until the uncertainty about the hearing threshold is sufficiently small. The fully probabilistic treatment of the estimation problem has some favourable properties:

  • An objective, information-theoretic criterion can be used to pick test tones such that the the uncertainty is decreased as fast as possible. This minimizes the required number of trials to reach the desired accuracy.
  • Prior knowledge about the user’s hearing threshold - for example based on age or medical history - can be leveraged to further decrease the number of required trials.
  • The complete threshold curve is inferred directly, instead of only inferring the thresholds at a set of standard frequencies.
  • The stopping criterium can be defined in an objective manner.
  • The method can be combined with other threshold estimation methods that take a probabilistic HT estimate as input.

Results

To demonstrate the method, we performed simulations in which we try to estimate an artifical hearing threshold curve. The figure below depics an example of the resulting ‘probabilistic’ audiograms after 7, 14, and 21 trials: 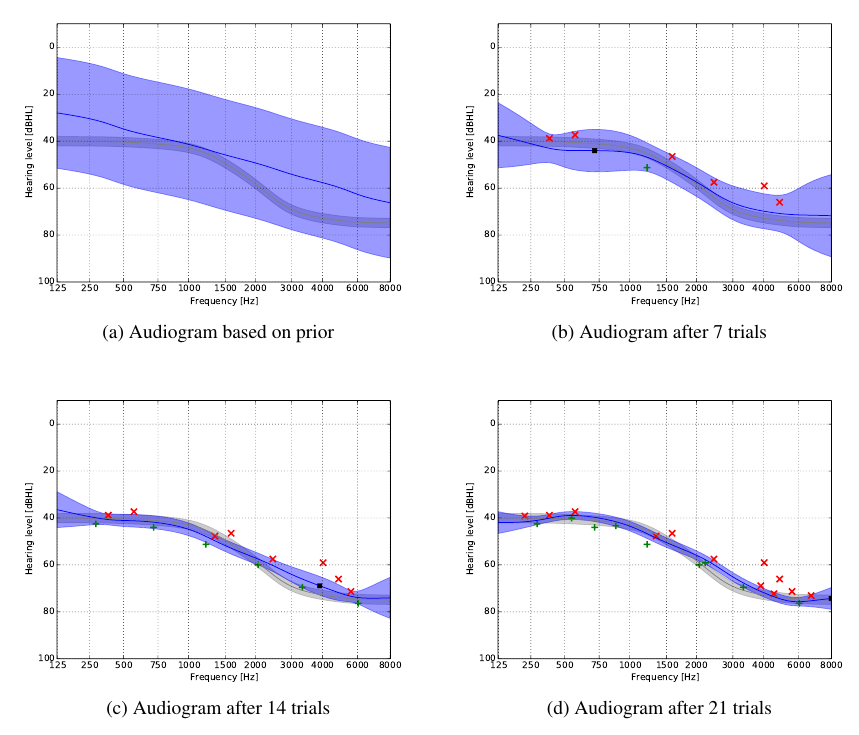png The grey curve depics the ’true’ hearing threshold curve and the grey area covers 2 standard deviations of the user’s response noise. The green plusses and red crosses represent test tones that were labelled as either audible (green) or non-audible (red). The blue line is the HT estimate based on the data so far, and the blue area depics 2 standard deviations of the estimate uncertainty. The rate of convergence obviously depends on the amount of noise in the response model. However, the method is robust in the sense that if the response model is sufficiently accurate, it will converge to the true hearing threshold curve in a minimum number of steps.

References

More details on this project are available in the following papers:

Participants