Problem Statement
The goal of scientific modeling is to find increasingly better models for given datasets. While the proposal of a new model is inherently human (creative) work, the right choice of framework may allow for automated derivation of efficient algorithms for model fitting and performance evaluation. Bayesian (probabilistic) reasoning offers such a principled framework for model specification, fitting and criticism [1]. Moreover, for a large class of models, Bayesian inference can be automatically derived. The field of probabilistic programming offers tools that rely on a variety of methods (e.g. automated derivation and Monte Carlo methods) that absolve the need for manual derivations. However, their generality often comes at the cost of considerable computational load.
The message passing paradigm offers a convenient method for leveraging model-specific structures, while remaining generally applicable. Message passing can be conveniently formulated on a Forney-style factor graph (FFG) representation of the model [2]. Inference tasks on the model can then be decomposed in local computations, represented by messages that flow across the graph. This locality allows for storing pre-computed message updates in a look-up table that can be re-used across models. Automated algorithm construction then amounts to scheduling these messages in the order required by the inference task (see also this conference paper at JuliaCon).
ForneyLab (GitHub) is introduced in this paper [5] as a novel Julia package that allows the user to specify a probabilistic model as an FFG and pose inference problems on this FFG. In return, ForneyLab automatically constructs a Julia program that executes a message passing-based (approximate) inference procedure. ForneyLab is designed with a focus on flexibility, extensibility and applicability to biologically plausible models for perception and decision making, such as the hierarchical Gaussian filter (HGF) [3]. With ForneyLab, the search for better models for perception and action can be accelerated (see also this conference paper at CCS).
Methods and Solution Proposal
An FFG offers a computational network representation of a probabilistic model, where edges represent variables and nodes capture probabilistic relationships between variables [4]. The figure below shows the FFG for the HGF and a message passing schedule for on-line state inference.
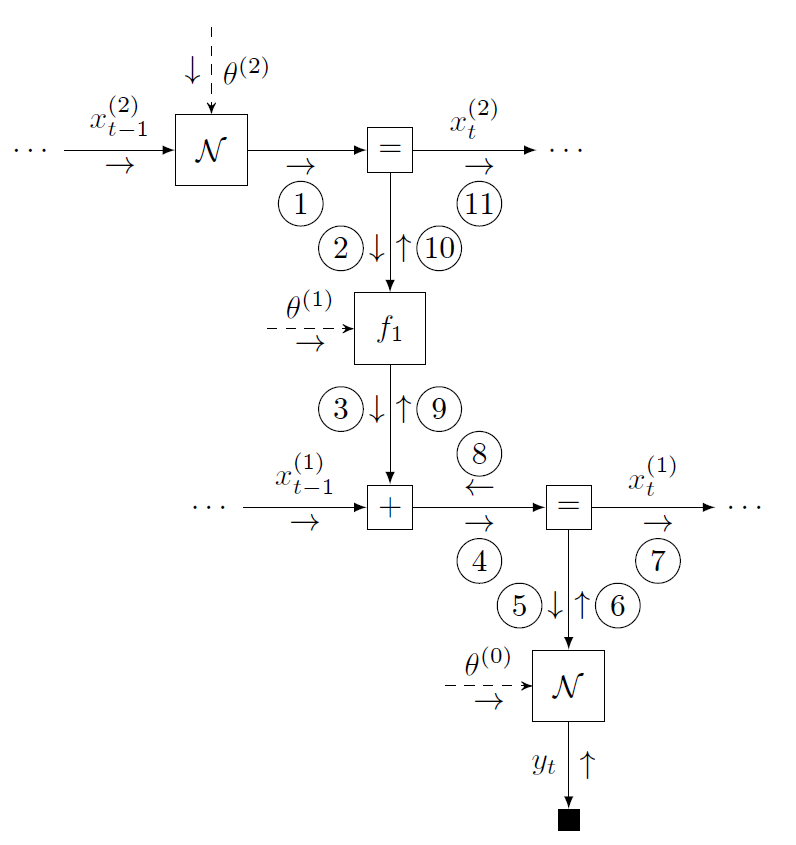
With ForneyLab, the automated derivation of this message passing algorithm may be completed in three phases. (1) The build phase specifies the model by a domain-specific syntax that (under the hood) constructs the model FFG. (2) The schedule phase specifies the inference problem. ForneyLab automatically constructs a message passing algorithm that computes the posterior marginal beliefs over the quantities of interest. (3) The infer phase parses and executes the automatically generated algorithm code and optional model performance metric. See the video below from JuliaCon for a quick introduction to ForneyLab.
Results
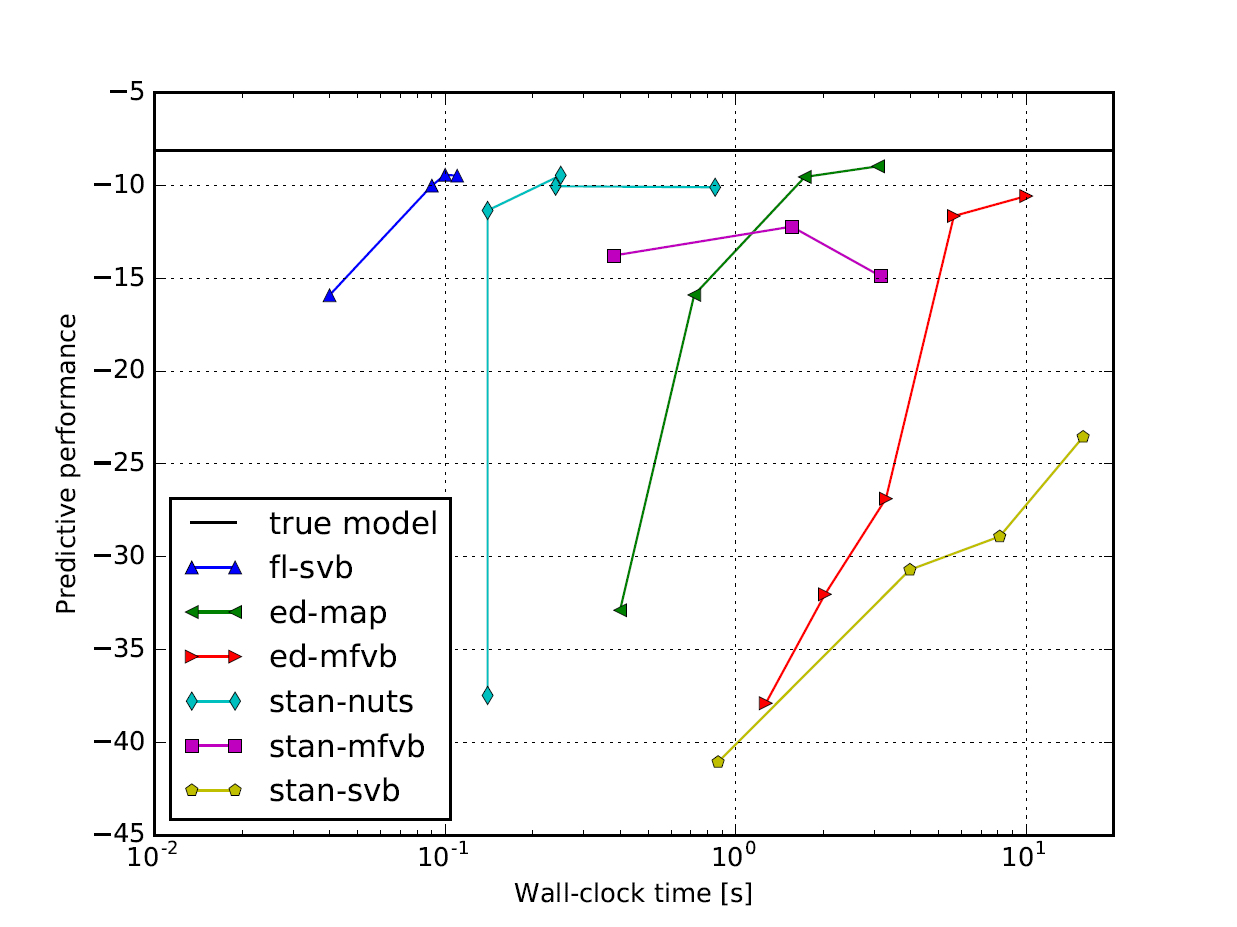
ForneyLab is especially potent when applied to time-series data. In this section we place ForneyLab within the time-performance landscape by comparing with Edward and Stan, two popular probabilistic programming toolboxes that employ automated differentiation and sampling-based inference. As an example application, we fit a random walk model to artificial observations and compare predictive performance on a hold-out set (see also this conference paper at ProbProg). The results are shown in the figure below, where it can be seen ForneyLab attains comparable performance in significantly less computation time [5].
References
[1] Blei, David M. “Build, compute, critique, repeat: Data analysis with latent variable models.” Annual Review of Statistics and Its Application 1 (2014): 203-232.
[2] Forney, G. David. “Codes on graphs: Normal realizations.” IEEE Transactions on Information Theory 47.2 (2001): 520-548.
[3] Mathys, Christoph D., et al. “Uncertainty in perception and the Hierarchical Gaussian Filter.” Frontiers in human neuroscience 8 (2014): 825.
[4] Loeliger, H-A. “An introduction to factor graphs.” IEEE Signal Processing Magazine 21.1 (2004): 28-41.
[5] Cox, M., van de Laar, T., de Vries, B. “A Factor Graph Approach to Automated Design of Bayesian Signal Processing Algorithms”, International Journal of Approximate Reasoning (2019), 10.1016/j.ijar.2018.11.002.